8. The Eighth Dimension – A Split When we describe infinity as being a “point” in the seventh dimension, we are only imagining part of the picture. If we’re drawing a seventh dimensional line, we need to be able to imagine what a different “point” in the seventh dimension is going to be, because that’s [...]
magnus-pedersen.dk
You are currently viewing the category archives of Physics
Category Archives: Physics
Dimensions #7
7. The Seventh Dimension – A Line In our description of the fourth dimension, we imagined taking the dimension below and conceiving of it as a single point. The fourth dimension is a line which can join the universe as it was one minute ago to the universe as it is right now. Or in [...]
Dimensions #6
6. The Sixth Dimension – A Fold What if you wanted to go back into your own childhood and visit yourself? We can imagine folding the fourth dimension through the fifth, jumping back through time and space to get there. But what if you wanted to get to the world where, for example, you had [...]
Dimensions #5
5. The Fifth Dimension – A Split One of the most intriguing aspects of there being one dimension stacked on another is that down here in the dimensions below we can be unaware of our motion in the dimensions above. Here’s a simple example: if we make a Möbius strip (take a long strip of [...]
Dimensions #4
4. The Fourth Dimension – A Line Okay. The first three dimensions can be described with these words: “length, width, and depth”. What word can we assign to the fourth dimension? One answer would be, “duration”. If we think of ourselves as we were one minute ago, and then imagine ourselves as we are at [...]
Dimensions #3
3. The Third Dimension – A Fold Imagining the third dimension is the easiest for us because every moment of our lives that is what we’re in. A three dimensional object has length, width, and height. But here’s another way to describe the third dimension: if we imagine an ant walking across a newspaper which [...]
Dimensions #2
2. The Second Dimension – A Split If we now take our first dimensional line and draw a second line crossing the first, we’ve entered the second dimension. The object we’re representing now has a length and a width, but no depth. To help us with imagining the higher dimensions, we’re going to represent our [...]
Dimensions #1
1. The first dimension – a line A second point, then, can be used to indicate a different position, but it, too, is of indeterminate size. To create the first dimension, all we need is a line joining any two points. A first dimensional object has length only, no width or depth.
Dimensions
0. A point (no dimension) We start with a point. Like the “point” we know from geometry, it has no size, no dimension. It’s just an imaginary idea that indicates a position in a system.
Final proof!
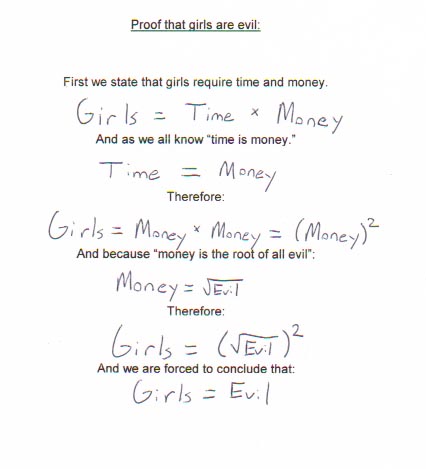
This is it! Isn’t it?